Volume Using Double Integrals

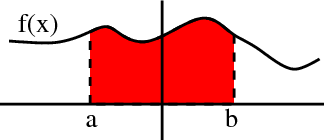
 You are probably familiar that in one-variable calculus, the integral 

∫baf(x)dx${\int }_a^{b}f(x)dx$ for positive f(x)$f(x)$ can be interpreted as the area under the curve f(x)$f(x)$ over the interval [a,b]$[a,b]$.

The integral is the area between the curve f(x)$f(x)$ and the x$x$-axis.

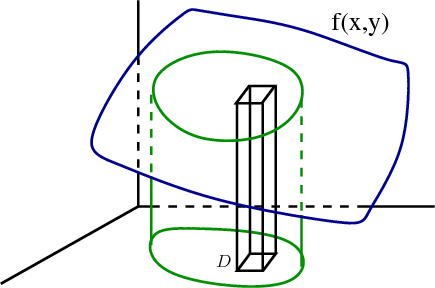
In the same way, the double integral ∬Df(x,y)dA${\iint }_{D}f(x,y)dA$ of positive f(x,y)$f(x,y)$ can be interpreted as the volume under the surface z=f(x,y)$z=f(x,y)$ over the region D$D$. Imagine that the blue object below is the surface z=f(x,y)$z=f(x,y)$ floating above the xy$xy$-plane. The double integral ∬Df(x,y)dA${\iint }_{D}f(x,y)dA$ can be interpreted as the volume between the surface z=f(x,y)$z=f(x,y)$ and the xy$xy$-plane, i.e, the “cylinder” above the region D$D$.

You can also see this from the Riemann sum approximating the integral

∑i,jf(xij,yij)ΔxΔy$$\begin{array}{r}\sum _{i,j}f(x_{ij},y_{ij})\mathrm{\Delta }x\mathrm{\Delta }y\end{array}$$

Each term in the Riemann sum is the volume of a thin box with base Δx×Δy$\mathrm{\Delta }x\times \mathrm{\Delta }y$ and height f(xij,yij)$f(x_{ij},y_{ij})$.

Hence, the total Riemann sum approximates the volume under the surface by the volume of a bunch of these thin boxes. In the limit as Δx,Δy→0$\mathrm{\Delta }x,\mathrm{\Delta }y\to 0$, we obtain the total volume under the surface over the region D$D$, i.e., ∬Df(x,y)dA${\iint }_{D}f(x,y)dA$.

The below applet illustrates how the volume of the boxes approaches the area under the surface as Δx$\mathrm{\Delta }x$ and Δy$\mathrm{\Delta }y$ decrease to zero.

If f(x,y)>g(x,y)$f(x,y)>g(x,y)$ can you see how the double integral

∬D(f(x,y)−g(x,y))dA$$\begin{array}{r}{\iint }_D(f(x,y)-g(x,y))dA\end{array}$$

is the volume between the surface z=f(x,y)$z=f(x,y)$ and the surface z=g(x,y)$z=g(x,y)$?

Example

Imagine if we had to find volume for 

x^2 + y^2 = 9

x^2 + y^2 + z^2 =9, and

z = 0. 

For rectangular coordinates, we can simply write this as,

For other coordinates we have,

Finally for spherical we have,

Example 2

Determine the volume of the region that lies behind the plane $x+y+z=8$ and in front of the region in the $yz$-plane that is bounded by $z=\frac{3}{2}\sqrt{y}$ and $z=\frac{3}{4}y$.

Here are the limits for each of the variables.

$$\begin{array}{c}0\le y\le 4\\ \frac{3}{4}y\le z\le \frac{3}{2}\sqrt{y}\\ 0\le x\le 8-y-z\end{array}$$

The volume is then,

$$\begin{array}{cc}V& =\underset{E}{\iiint }dV=\underset{D}{\iint }\left[{\int }_0^{8-y-z}dx\right]dA\\ & ={\int }_0^4{\int }_{3y/4}^{3\sqrt{y}/2}8-y-zdzdy\\ & ={\int }_0^4{\left(8z-yz-\frac{1}{2}{z}^2\right)|}_{\frac{3y}{4}}^{\frac{3\sqrt{y}}{2}}dy\\ & ={\int }_0^{4}12y^{\frac{1}{2}}-\frac{57}{8}y-\frac{3}{2}{y}^{\frac{3}{2}}+\frac{33}{32}{y}^{2}dy\\ & ={\left(8y^{\frac{3}{2}}-\frac{57}{16}{y}^2-\frac{3}{5}{y}^{\frac{5}{2}}+\frac{11}{32}{y}^3\right)|}_0^4=\frac{49}{5}\end{array}$$