Finding Minimum and Maximum for a function

 A local minimum/maximum is a point in which the function reaches its lowest/highest value in a certain region of the function. In formal words, this means that for every local minimum/maximum x, there is an epsilon such that f(x) is smaller/greater than all values f(y) for all y that have distance at most epsilon to x. That looks very complicated but it does mean as much as f(x) is the smallest/largest value for all points close to x. There might be values, however, that are smaller/larger than the local minimum/maximum, but they are further away.

The global minimum is the smallest value the function takes on in its entire domain. Equivalently, the local maximum is the largest value of the function. Therefore, every global extreme point is also a local extreme point, but the opposite is not true.

At a local minimum, the function changes direction. This is because it is the lowest point in its neighborhood. Therefore the slope of the function goes from negative to positive, since the function was decreasing until it reached the minimum and then it started increasing again. This means that in the local minimum, the slope is equal to zero, and hence the derivative of the function must be equal to zero in the point that is the minimum. The same holds for the local maximum of a function, since there the function goes from increasing to decreasing.

Therefore, to find the location of the local maxima and local minima you have to solve the equation f'(x) = 0. Therefore you have to first find the derivative of the function. If you are not familiar with the derivative, or if you would like to know more about it I recommend reading my article about finding the derivative of a function. For this article I assume the derivative is known.

As an example, we will use the function f(x) = 1/3 x3 - 4x. First we calculate the derivative of the function, which is:

f'(x) = x2 - 4

Then we solve f'(x) = 0:

x2 + 4 = 0

This gives x = 2 or x = -2. Therefore we know that the local extrema are located at 2 and -2. We fill both in to determine the value of the extrema:

1/3 23 - 4*2 = 8/3 - 8 = -16/3

1/3 (-2)3 - 4*-2 = -8/3 + 8 = 16/3

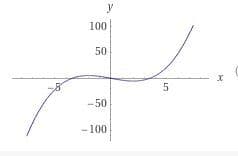
Then we plot the function.

Plot of 1/3*x^3 -4x

As you can see in the plot, at x=-2 we have a local maximum with value 16/3. At x=2 we have a local minimum with value -16/3. We can also see however, that both local extrema are not global, since clearly there are points at which the function value is smaller than -16/3 and also there are points at which the function value is larger than 16/3. This means that the global minimum and global maximum do not exist, even though there do exist local extrema, which can happen.

Solving f'(x) = 0

Here, f'(x) was a quadratic function, which means we had to find the roots of a quadratic function to find the local extrema. Here I did not go deep into how I did solve this, but I did write an article about how to solve these kind of equations.